Static Thread Mapping for High Concurrency XGBoost Inference Servers

Introduction

With the proliferation of machine learning (ML) models in all aspects of business, model serving has become a significant area of focus. The rise of high-concurrency (near) real-time ML applications has made minimizing latency a critical priority. For tabular models, gradient boosting frameworks like XGBoost continue to be the de facto standard. To run these models for real-time applications, tuning how the application and the server interact is crucial. Most modern servers use default task scheduling policies and often employ oversubscription to increase core utilization and reduce idling, the combination of which can significantly degrade performance of multi-threaded workloads if not managed carefully.

To mitigate some of these challenges, binding application threads to processor threads, a practice known as thread mapping, has been extensively studied to improve performance for general applications. Only recently, the performance benefits of simple thread mapping heuristics to generic ML algorithms has been studied, showing promising results¹. With no shortage of XGBoost inference servers out in the wild, all sharing a repeatable execution flow pattern, there is an opportunity to develop a strategic static thread mapping policy that can be applied across a wide range of use cases.

In this blog, we demonstrate a two-stage framework, Tuna (a portmanteau of tuning affinity), that implements a thread-to-core mapping specifically targeting the online XGBoost inference pattern running on a multi-threaded, multi-worker server hosted on a multi-core machine. The offline phase solves an Integer Linear Program (ILP), given some user-defined specifications while enforcing load balancing constraints that are based on workload characteristics of the pattern. This joint formulation combines the locality advantages of tried-and-tested static mapping heuristics with load balancing features that are lacking in the default scheduler. The online phase instantiates the server and binds the server threads to the respective cores prior to serving requests.

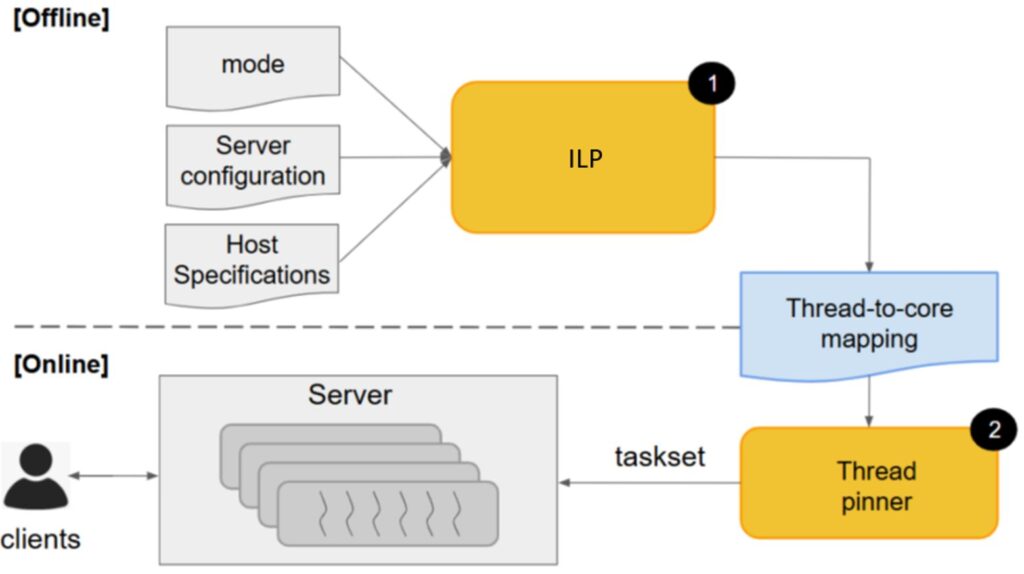
Read about troubleshooting memory errors in Python parallel processing

Background

Concurrent XGBoost Servers

Traditional web servers used the forking model to handle concurrency; a parent process accepts client connections and forks a child to handle each request. As concurrency grows, system overhead grows with more forked system calls, initial page faults, and protection faults due to the copy-on-write at fork. Instead, modern frameworks have adopted the pre-fork model; Gunicorn (Python), Unicorn (Ruby), and Apache HTTP server² all fork multiple processes at server instantiation, inheriting identical copies of memory items to serve to clients in parallel. XGBoost is an optimized gradient boosting algorithm used for machine learning tasks like regression and classification. It utilizes Open Multi-Processing (OpenMP)³ for parallelization, making it truly multi-threaded even in the context of single-threaded languages like Python. In this blog, we consider serving XGBoost via a Gunicorn server. We set the OMP_NUM_THREADS⁴ environment variable prior to starting the server to have a fixed number of workers, each with an independent and equally sized OpenMP thread pool for executing the XGBoost model.

Linux Scheduling

The default scheduler in Linux, the Completely Fair Scheduler (CFS), was introduced in Linux 2.6.23. On multi-core systems, each core maintains a runqueue that orders tasks assigned to it based on a dynamic value, the virtual runtime (vruntime). To ensure fairness, CFS prioritizes running tasks with lower vruntime (underserved tasks) so that tasks have a fair share of the processor. Periodically, CFS performs load balancing to ensure that tasks are evenly distributed across cores.⁵

Advantages

Disadvantages

All user threads get a fair share of the processor Load balancing across cores

Agnostic of thread memory sharing characteristics, leading to contention (memory-independent threads scheduled on the same core now compete for cache resources) or loss of locality (memory sharing threads scheduled on distant cores) Agnostic of thread workload; may schedule multiple high-load threads on a core despite equal thread counts on all cores Periodic load balancing leads to thread migrations, resulting in cache misses and higher memory latencies

Thread Mapping Policies

Thread mapping typically falls under two broad categories: static and dynamic.

Static	Dynamic
Applies a fixed thread-to-core binding throughout the life of the application Suitable for applications with predictable memory and workload characteristics Easy to implement	Periodically updates thread-to-core mapping at runtime Suitable for long running applications where memory access and workload behaviors change over time Requires running daemons to frequently gather thread statistics and re-compute mappings

Due to the short and repeatable nature of an inference request, we focus our attention on the static policy, the most widely used being compact, scatter, and round-robin.

Compact	Scatter	Round Robin
Groups threads logically close Low memory latency for threads that frequently access shared memory	Spreads threads as logically far as possible High memory bandwidth for threads that do not share memory	Places threads sequentially across available cores in a cyclic manner Suitable for multi-process applications but does not consider workload characteristics

Compact and Scatter do not generalize to multi-process applications. For example, if we set a mapping rule by setting the OpenMP environment variable OMP_PROC_BIND and start a multi-worker server, each worker will independently inherit the same mapping rule at compile time. This leads to all workers binding their threads to cores in the same pattern, resulting in non-uniform utilization of cores.

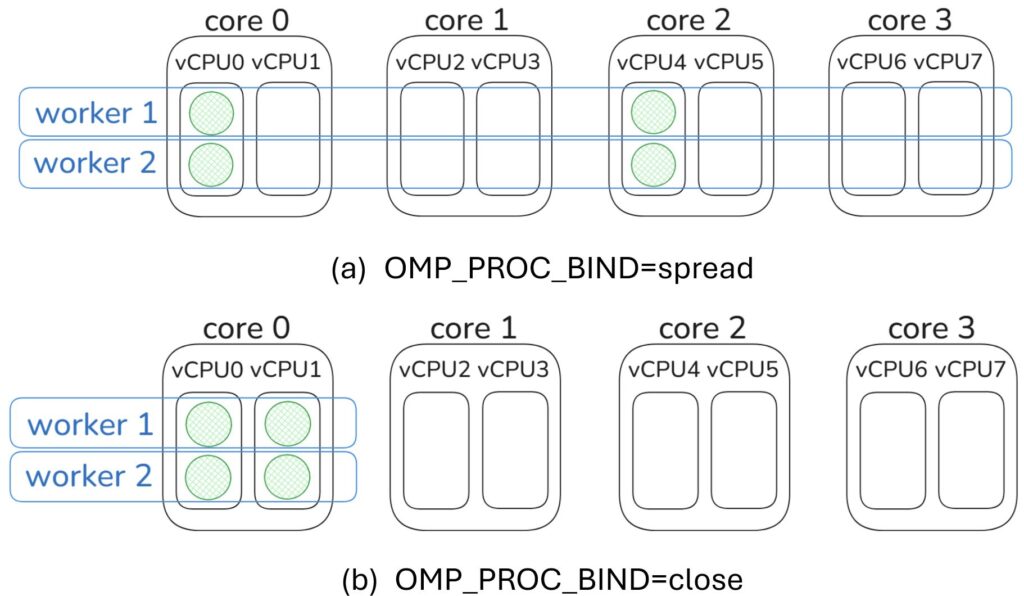
Round Robin is suitable for multi-process applications, however it does not account for thread workload which can lead to a couple of bottlenecks. When all workers share similar workload patterns, Round Robin repeatedly places high load threads on the same core if the number of worker threads divide cores. Second, if the number of cores do not divide total threads, Round Robin distributes remaining threads unfairly.

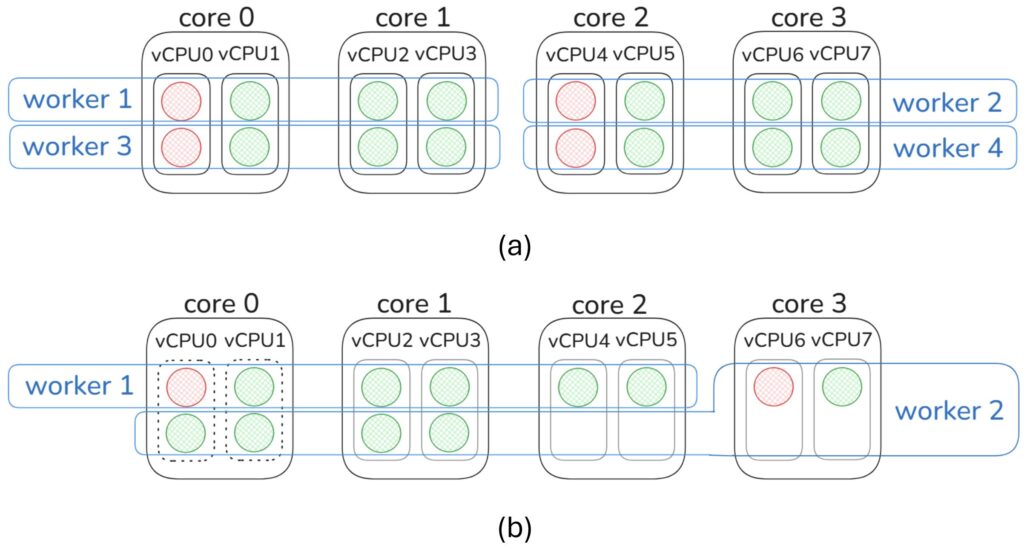
Formulation

To jointly account for the characteristics of the inference pattern and the above four strategies, we formulate a binary Integer Linear Program (0-1 ILP). A binary ILP is a type of mathematical optimization where decision variables are strictly 0 or 1, with a linear objective function to be maximized subject to a set of linear constraints.

Notation	Definition
\( W \)	Number of server workers
\( T \)	Number of OpenMP threads per worker
\( C \)	Number of logical cores
\( v \)	Number of logical cores per physical core
\( w \in \{ 0, \dots, W-1 \} \)	Index and set of workers
\( t \in \{ 0, \dots, T-1 \} \)	Index and set of threads for some worker; t=0 indicates a main thread
\( c \in \{ 0, \dots, C-1 \} \)	Index and set of logical cores
\( x \in \{ 0, \dots, \frac{C}{v} – 1 \} \)	Index and set of physical cores
\( d_{c,c’} \)	Distance between c,c′
\( Y_{w,t,c} \)	Binary decision variable for thread t of worker w assigned to c
\( L(L^+) \)	Lower limit of threads assigned to each logical(physical) core
\( U(U^+) \)	Upper limit of threads assigned to each logical(physical) core

ILP assumptions:

• System is homogenous (cores are functionally equivalent).
• Each worker handles equivalent load over time.
• The main thread of a worker handles a higher workload than peer threads, managing both model and non-model execution tasks.

ILP inputs:

• System core configuration; number of physical and logical cores.
• Server configuration: worker count and OpenMP thread count per worker.
• Heuristic mode for the ILP to solve towards; scatter or compact.

The ILP is parameterized by core-to-core distances using a heuristic proxy for thread communication latency. Suppose threads \( t,t’ \) are running on cores \( c,c’ \) respectively and \( t \) is accessing a word stored on \( t’ \) local caches. The process involves \( c \) generating a memory address for the word and issuing a read/write request that follows down the memory hierarchy until there is a hit. Thus, a conservative proxy for logical distance between the two cores, denoted \( d_{c,c’} \), can be the number of clock cycles to access the highest cache level shared by them. As a rough rule of thumb⁶, \( d_{c,c’}=4 \) if this is L1, \( d_{c,c’}=10 \) if L2, \( d_{c,c’}=50 \) if L3, \( d_{c,c’}=200 \) if L4, and \( d_{c,c’}=1 \) if \( c=c’ \).   

The following constraints jointly consider across-worker and within-worker thread relationships. Constraint (1) ensures that each thread can only be assigned to a single core. Constraint (2) ensures that given \( W \leq C \), all equally ranked threads across workers are assigned to a unique core relative to each other; this mitigates the risk of all main (or equally ranked) threads across workers contending for the same core. Constraint (3) ensures that given \( T \leq C \), all threads within a worker are assigned to a unique core relative to each other; this mitigates the risk of within-worker thread starvation.

\begin{equation}
\sum_{c}Y_{w,t,c}=1 \quad \forall w,t
\tag{1}
\end{equation} \begin{equation}
\sum_{w}Y_{w,t,c} \leq 1 \quad \forall t,c
\tag{2}
\end{equation} \begin{equation}
\sum_{t}Y_{w,t,c} \leq 1 \quad \forall w,c
\tag{3}
\end{equation}

Given that main threads have the highest within-worker workload and are independent of each other, we consider maximally spacing main threads across cores. We model the logical distance between two arbitrary main threads \( \{t=0|w,t’=0|w’\} \) that are mapped to two distinct cores \(c,c’\) respectively as (the linearization of binary products is omitted for brevity)

\begin{equation}
dist \left((t=0|w,c),(t’=0|w’,c’)\right)=\left( \sum_{w} Y_{w,t=0,c} \right)\left( \sum_{w} Y_{w,t=0,c’} \right)d_{c,c’}
\tag{4}
\end{equation}

Finally, we want to maximize the total logical distance across all main threads and add this to the objective function

\begin{equation}
f_{main}=\sum_{c}\sum_{c’>c}dist\left((t=0|w,c),(t’=0|w’,c’)\right)
\tag{5}
\end{equation}

We model thread dependencies and give users the flexibility to choose one of two modes to solve the mapping: scatter or compact. Scatter (Compact) mode will solve for a mapping that maximizes (minimizes) logical distances between within-worker threads. The logical distance between two threads within a worker, \(t \neq t’|w\), that are mapped to cores \(c,c’\) is

\begin{equation}
dist\left( (t|w,c),(t’|w,c’) \right)=\left( \sum_{t} Y_{w,t,c} \right)\left( \sum_{t} Y_{w,t,c’} \right)d_{c,c’}
\tag{6}
\end{equation}

Finally, we model the total logical distance between all within-worker threads over all workers and add it to the objective to be maximized (minimized) under Scatter (Compact) mode.

\begin{equation}
f_{mode}=(-1)^{\mathbb{1}(compact)} \sum_{w}\sum_{c}\sum_{c’>c}dist\left( (t|w,c),(t’|w,c’) \right)
\tag{7}
\end{equation}

Next, we formulate constraints that enforce balanced workload and volume across logical cores; such constraints mitigate the risks of unbalanced workload distribution that CFS and Round Robin are subject to, given their application-agnostic nature. We consider three scenarios

1. \(WT < C\): application threads are exceeded by cores.
2. \(WT \mod C=0\): application threads are divisible by cores.
3. \(WT > C\) and \(WT \mod C>0\) application threads exceed and are not equally divisible by cores.

We define a fair lower and upper bound \(L,U\) of thread volume that can be assigned to each core

\begin{equation}
\left\lfloor\frac{WT}{C} \right\rfloor=L \leq \sum_{w}\sum_{t}Y_{w,t,c} \leq U=\left\lceil \frac{WT}{C}\right\rceil \quad \forall c
\tag{8}
\end{equation}

Constraint (8) is sufficient for scenario 1 because each core is assigned 0 or 1 threads. It is also sufficient for scenario 2 because \(L=U\) and thus each core is assigned an equal number of threads. Scenario 3 requires additional consideration because there will be a remainder of \(r=WT \mod C\) cores that must be assigned \(U\) threads and \(C-r\) cores that must be assigned \(L\) threads. This allocation is unaccounted for by Round Robin but is non-trivial given that main threads are heavier loaded than peer threads.

Scenario 3 requires consideration of two cases:

1. \(W \leq C-r\): worker count is equal to or exceeded by the number of cores that can be assigned \(L\) threads. \(W\) cores will be assigned a main thread and thus it is feasible and beneficial to assign these cores a total of \(L\) threads (1 main thread and \(L−1\) peer threads) while the remaining cores can be assigned \(U\) peer threads so as not to over assign workloads.
2. \(W>C-r\): worker count exceeds number of cores that can be assigned \(L\) threads. \(W\) cores will be assigned a main thread but not enough remaining cores to ensure that these \(W\) cores will only be assigned \(L\) threads. In fact, the minimum number of cores which must be over assigned workload (\(U\) total threads, including a main thread) is \(max\{0,W-C+r\}\).

We introduce binary auxiliary variables, \(M_c\), indicating whether some main thread is assigned to a core \(c\)

\begin{equation}
M_c \geq Y_{w,t=0,c} \quad \forall w,c
\tag{9}
\end{equation} \begin{equation}
M_c \leq \sum_{w} Y_{w,t=0,c} \quad \forall c
\tag{10}
\end{equation}

Constraint 9 ensures that \(M_c\) is 1 if any main thread is assigned to core \(c\) while constraint 10 ensures that \(M_c\) is 0 if none of the main threads have been assigned to \(c\). For each core, we can now indicate the event \(E_c=E_c^1 \cap E_c^2\) where \(E_c^1:=\) core \(c\) is assigned \(U\) total threads and \(E_c^2:=\) core \(c\) is assigned a main thread:

\begin{equation}
\mathbb{1}(E_c)=\left( \sum_{w} \sum_{t} Y_{w,t,c} – L \right)M_c \quad \forall c
\tag{11}
\end{equation}

Given that (11) is bound by 0 and 1, we sum the total count of events \(E_c\) over all cores and bound it

\begin{equation}
\sum_{c} \mathbb{1}(E_c) \leq max \{ 0, W-C+r \}
\tag{12}
\end{equation}

Using near similar reasoning, we can derive constraints that enforce balanced workload and volume across physical cores, however we omit them for brevity.

Experimental Setup

We implement a static application pattern (P) running on a homogenous multi-core machine (H) across three sources of variation: server worker-thread configuration (S), model instance (M), request size (B).

Component	Specifications
P	When a request is routed to a worker, the following sequence of tasks is executed: 1. payload deserialization (single-threaded) 2. data-type conversions (single-threaded) 3. DMatrix declaration for XGBoost input (multi-threaded) 4. Compute model predictions (multi-threaded) 5. Compute Shapley feature contributions (multi-threaded)
H	All experiments are deployed independently to an Azure k8s cluster and run on a Standard_D32ds_v4 compute node that includes a single socket Intel Xeon Platinum 8272CL @ 2.60GHz processor with 16 physical cores and 32 logical cores. The operating system is Linux 5.15.
S	Server worker and model thread counts vary over 36 configurations, \(\{2,4,6,8,12,16\}\) gunicorn workers \(\times\{2,4,6,8,12,16\}\) OMP threads, resulting in 20(16) thread-to-core over(under) subscribed configurations (An environment is oversubscribed if workers × threads/worker > 32 logical cores).
M	Models vary across three sizes*: 1. Small: 29 features trained on the Credit Card Fraud Detection 2. Medium: 155 features trained on the Loan Defaulter 3. Large: 784 features trained on the MNIST in CSV
B	Payloads vary across three different batch sizes: 1. Small: 100 records/ request 2. Medium: 500 records/ request 3. Large: 1,000 records/ request

We consider a unique application to be any fixed instance of {S,M,B}, resulting in 324 \( (36 \times 3 \times 3)\) applications. Each application is ran independently under three different scheduling policies; CFS, Round-Robin, and Tuna, resulting in 972 application scenarios. Each scenario is load tested independently over 5 trials, each with 1,000 concurrent requests; the server-side runtime is logged for each request. For each trial, we compute the p99 of the 1,000 runtimes and finally compute the average p99 runtime for each scenario.

Results and Analysis

Runtime Speedup

After obtaining the 972 average p99 runtimes, we compute aggregate speedups of our method relative to Round Robin and CFS and averaging over all three sources of variation. In summary, our method achieves a runtime speedup of \(1.15 \times\) and \(1.13 \times\) over CFS and Round Robin respectively.

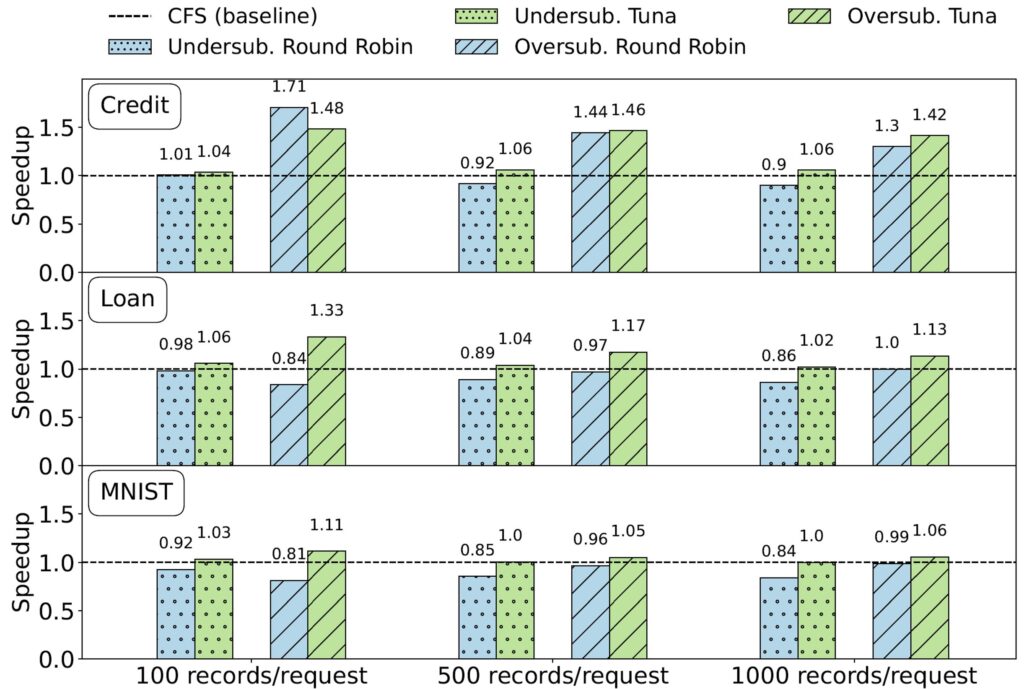
Referring to the above figure, Tuna consistently outperforms CFS across all model and batch variations, at worst case matching CFS performance for large model and batches in undersubscribed groups. When the model size is small, Round Robin shows comparable performance to Tuna across all batch sizes and outperforms Tuna when batch size is small and the server is oversubscribed, but its performance significantly degrades for all other groups. The results reveal a diminishing trend in gain for Tuna as both the model and batch sizes are increased, suggesting that when keeping hardware cache sizes constant, the benefits of thread binding become less significant as the memory footprint of your application grows.

Server Configurations

To understand performance variations within under and oversubscribed groups in finer detail, we illustrate the application scenarios with the medium model processing small batch sizes under all 36 server configurations. The below figure overlays 1) a scatterplot of p99 runtimes of the 5 trials for each policy for all 36 server configurations with 2) a line plot representing the average p99 runtime of the trials. The grey(white) regions represent under(over) subscribed configurations.

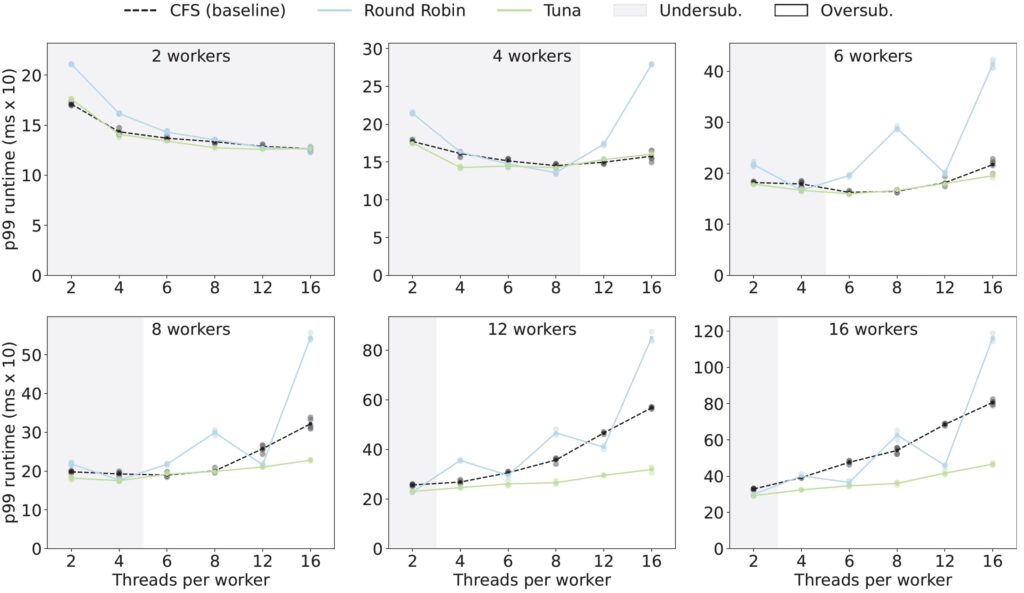
Intuitively, the undersubscribed regions show trends of decreasing (improving) runtime while the oversubscribed regions show trends of increasing (degrading) runtime for all policies; enough cores are available to run all threads, enabling more parallelism for each additional thread with minimal contention. In oversubscription cores become saturated, increasing contention with each additional thread. While Tuna provides gains over both policies in undersubscribed ranges, Tuna reduces the rate of performance degradation as oversubscription grows.

Round Robin shows significantly higher performance variability across server configurations, most evident by certain spikes. As expected, these spikes occur when either the model thread count divides the number of cores or the number of cores does not divide total application threads (in some case both), causing overutilized cores to bottleneck performance as described earlier.

Inference Pipeline Stages

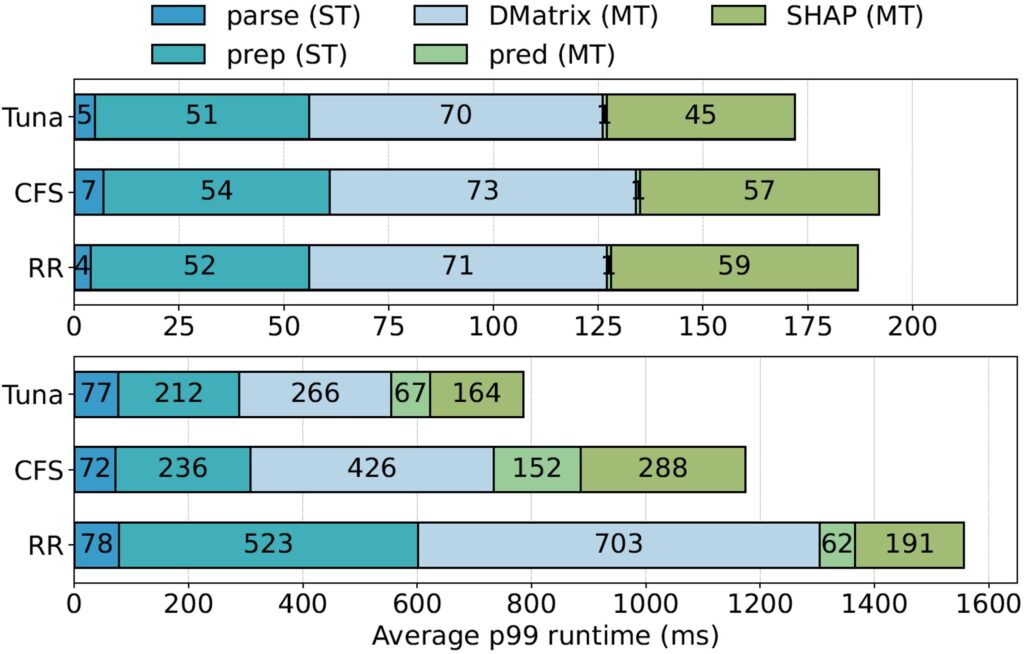
To understand the performance gains within the inference pipeline, we individually profiled the 5 stages of the pipeline. We illustrate performance profiles for the medium model processing small batches running on both the \(4 × 4\) (undersubscribed) and \(16 × 16\) (oversubscribed) server configurations. The average p99 runtime of each stage is computed and illustrated below.

In the undersubscribed runs, all policies show comparable performance across single-threaded stages with Round Robin showing marginal gains during the data preparation stage. Across multi-threaded stages, Tuna significantly outperforms both policies during the SHAP stage which contributes to the majority of performance gain. In the oversubscribed runs, Tuna largely outperforms both policies during all stages while Round Robin consistently under performs.

Closing Remarks

In this blog we showed how a strategic thread mapping tailored to your application pattern can improve performance. However, there are a few caveats to consider. First, threads inherit affinity. After starting the server and pinning threads appropriately, overtime your application may either destroy and recreate threads or even exit and fork new workers (Gunicorn graceful shutdowns). If left unchecked, the new affinities are no longer optimal. Second, make sure to run your application on a dedicated resource. Sharing a deployment resource with other applications degrades the benefit of pinning, as the application is now competing with other applications that are out of your control for the same resources.

References

1. Matheus S. Serpa, Arthur M. Krause, Eduardo H. M. Cruz, Philippe Olivier Alexandre Navaux, Marcelo Pasin, and Pascal Felber. Optimizing machine learning algorithms on multi-core and many-core architectures using thread and data mapping. In 2018 26th Euromicro International Conference on Parallel, Distributed and Network based Processing (PDP), pages 329–333. IEEE, 2018 ↩︎
2. Apache MPM prefork. https://httpd.apache.org/docs/2.4/mod/prefork.html ↩︎
3. The OpenMP API specification for parallel programming. https://www.openmp.org ↩︎
4. OMP_NUM_THREADS. https://www.openmp.org/spec-html/5.0/openmpse50.html ↩︎
5. Andrew S. Tanenbaum and Herbert Bos. Modern Operating Systems, Fourth Edition. Pearson, 2015. p. 749 ↩︎
6. Randal E. Bryant and David Richard O’Hallaron. Computer Systems: A Programmer’s Perspective. Prentice Hall, 2011. p. 643,660-661 ↩︎