Person to person communication is incredibly nuanced. Beyond the words we choose, our tone, body language, and facial expressions all communicate a great amount of information about how we feel and what we truly mean. When answering a question, all of these factors impart a level of confidence to our response which can be used to gauge how trustworthy that answer is. People naturally signal uncertainty to others through language, and offer alternative answers when unsure of a single response.

On the other hand, machine learning models for classification or regression problems typically output only a single prediction. That prediction rarely comes with a meaningful notion of the model’s confidence level. This is a grave departure from the signaling that humans expect to receive when communicating, and greatly degrades the trustworthiness of model predictions.
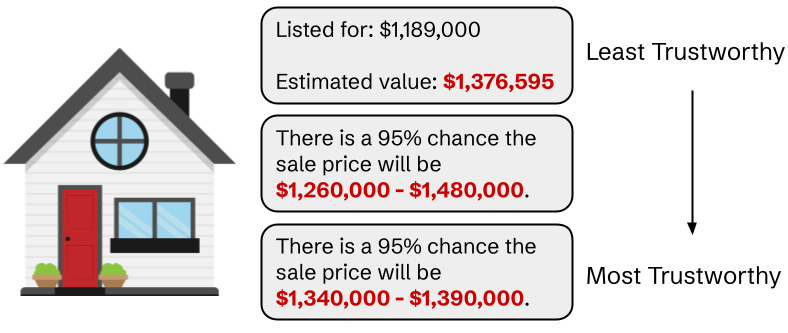
Quantifying uncertainty is a crucial aspect of informed decision making. Imagine you were looking to buy a house and used an online machine learning tool that estimated the selling price. Would you be prepared to make a purchase offer if the estimate was a single number with no additional information to back it up? Would you be reassured if there was a 95% confidence interval that showed a tight range of a few tens of thousands of dollars? For equivalent correctness guarantees, tighter ranges of possibilities or fewer alternative answers make the estimates more trustworthy to decision makers.
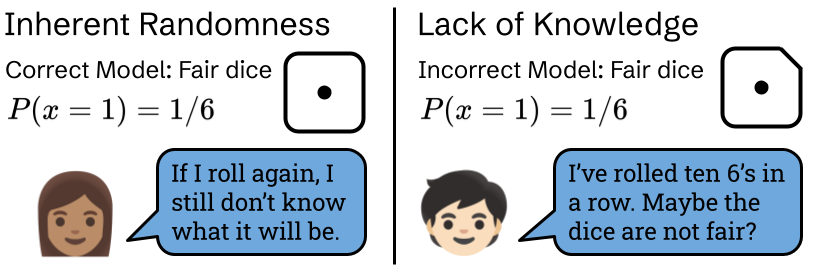
Generally, scientists and statisticians consider two types of uncertainty. First, there is inherent randomness which cannot be predicted by our model of the system, like rolling fair dice. With inherent randomness we cannot, for all practical purposes, know what the outcome will be ahead of time. Second, uncertainty can also come from our lack of knowledge — factors which haven’t been accounted for, but could in practice be included in our model. Imagine now that our dice are not fair — they come up as sixes more often than ones. Modeling the dice as fair by predicting equal likelihoods for each outcome would be a misspecification, but one that we could correct after observing that sixes systematically appear more than ones. However, once our model is updated to predict sixes as more likely, any given roll could still come up as a one, showing that there is still inherent randomness.
There have been numerous approaches to quantifying uncertainty with machine learning models over time. Some require changing the model architecture or training algorithm. Some require fine-tuning a trained model, or adding additional network components. These kinds of changes are generally undesirable because they add costly computation steps, restrict the modeler’s choices in some way, or more technically because they rely on assumptions about the distribution of data which are unlikely to be true in the real world.
One method has stood out in recent years due to its wide applicability — it works with any pre-trained model directly, provides rigorous guarantees on finite datasets, and does not make unreasonable assumptions about data distributions. The main idea behind conformal prediction is that models which output a single (point) prediction do a poor job of conveying when the model is confident or not. Model uncertainty can be quantified by having the model output several likely options when it is less confident, similar to how humans offer alternatives. That is, instead of a point prediction, the model outputs a prediction set with size calibrated to its confidence.
Conformal Prediction
Conformal prediction is a general purpose method for transforming heuristic notions of uncertainty into rigorous ones through the use of calibrated prediction sets.1 Considering a classification problem with input \(x\) associated to label \(y\) under the joint distribution \(\mathbb{P}\), a conformal predictor outputs a prediction set \(\mathcal{C}(x)\) containing the most likely class predictions. The hallmark of conformal prediction is its statistical guarantee of correctness; conformal sets will only fail to contain the ground truth with a pre-specified error rate \(\alpha\). This is referred to as the coverage guarantee,
\begin{equation}
\mathbb{P}[y \in \mathcal{C}(x)] \geq 1 – \alpha,
\tag{1}
\end{equation}
which tells us that the correct label \(y\) is contained in the prediction set at least a fraction \(1-\alpha\) of the time. The coverage guarantee is important for ensuring reliability of prediction sets for decision making, and is based on remarkably few assumptions. Since this guarantee is at the center of uncertainty quantification with conformal prediction, let us spend some time discovering how conformal sets can be generated from any pretrained classifier.
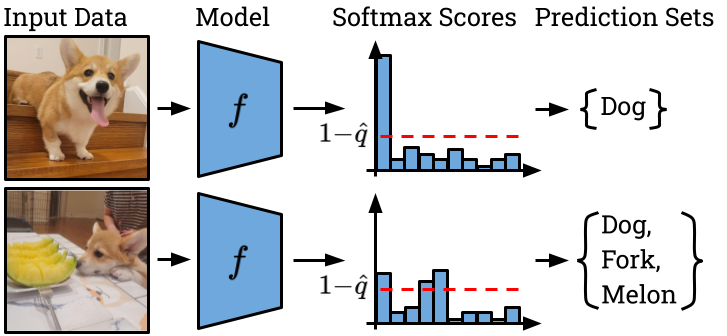
Often, the softmax outputs of a classifier are misconstrued as the model’s estimate of the probability that each possible class is the correct label. While softmax outputs do sum to one by construction, they should not necessarily be considered as probabilities unless they are properly calibrated. Proper calibration means that out of all examples where the model predicts with 50% confidence, 50% of those predictions should be correct. Similarly, for every confidence level (e.g. 10% confidence, 20% confidence, etc.), the predictions actually turn out to be correct that fraction of the time. Some training objectives, like the cross-entropy loss, do encourage the model to output accurately calibrated probabilities, but it is well-known that large neural networks tend to be greatly over-confident.2 Hence, to achieve the coverage guarantee, it is not enough to add classes \(y\) to the prediction set \(\mathcal{C}(x)\) until the softmax weight of added classes is at least \(1-\alpha\). We must first ensure that the model’s predictions are properly calibrated using a held-out calibration set.
Conformal prediction prescribes a four-step method for constructing prediction sets that satisfy coverage at any desired error level \(\alpha\) by calibrating a model’s built-in heuristic notion of uncertainty. The steps are shown in the diagram below.
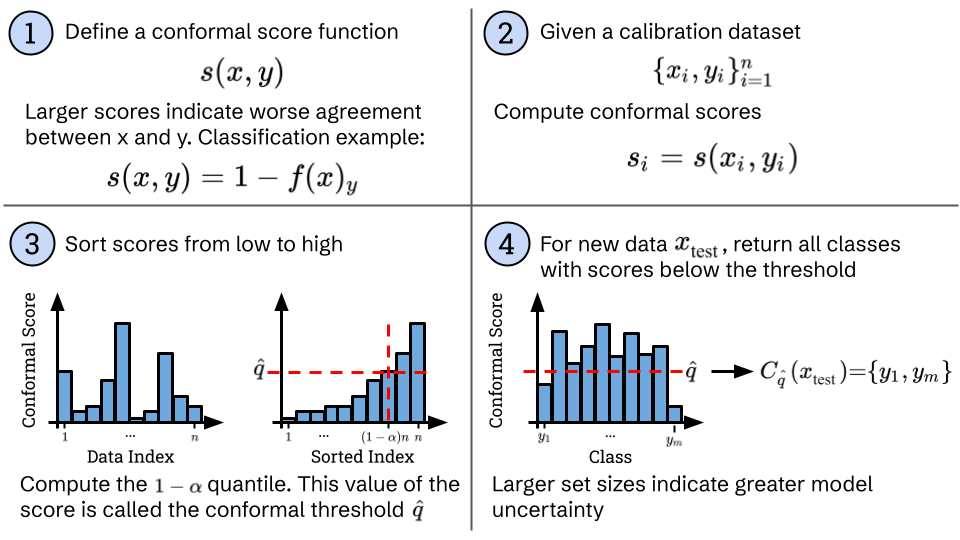
First, we define a conformal score function \(s\) acting on a data input \(x\) and class \(y\) where larger scores indicate worse agreement between \(x\) and \(y\). Perhaps the simplest conformal score for classification is to take \(1-f(x)_y\), where \(f(x)_y\) is the model’s softmax output for class \(y\). Then, when the model believes \(y\) is highly likely to be the correct class for \(x\), \(1- f(x)_y\) will be close to zero indicating good agreement between \(x\) and \(y\). When \(y\) is unlikely under the model, \(1- f(x)_y\) will be close to one indicating worse agreement.
Second, using a labeled calibration dataset \(\{x_i, y_i\}\) of size \(n\), we compute the conformal scores \(s(x_i, y_i)\) on all datapoints. Third, we sort those scores from low to high and find the \(1-\alpha\) quantile. The score at that quantile is sometimes called the conformal threshold \(\hat q\). It serves to calibrate the conformal score since it is computed from a fresh calibration dataset.
With calibration done, the final step is to use the threshold to generate prediction sets for any new datapoints at test-time. Any classes where the conformal score falls below the threshold are added to the set:
\mathcal{C}_{\hat q}(x) = \{y \mid s(x, y) < \hat q \}.
\tag{2}
\end{equation}
When the model is very confident in one class, only that class will have a score below the threshold and the model will output a singleton set. For more uncertain predictions, several classes will be added. Hence, the size of the prediction set directly communicates the model’s uncertainty.
Remarkably, conformal prediction sets will obey the coverage guarantee for test data with the sole assumption being that the calibration and test data are exchangeable. This is a technical condition, but notably it is weaker than the more familiar condition that data is i.i.d. – anytime that data is i.i.d. it will also be exchangeable.
With these four simple steps requiring only a bit of fresh calibration data, any model that outputs uncalibrated point predictions can be transformed into a model that quantifies its uncertainty with rigorous guarantees on coverage. As mentioned, conformal prediction does not make assumptions on the model or its training data. The model is treated as a black box — it can have any architecture and learning objective, and is not structurally modified. It is also worth emphasizing that the calibration and test data do not need to be similar to the training data – a model trained on data from one distribution would end up being miscalibrated on test data from another distribution, but conformal prediction explicitly includes a calibration set to remove any dependence on training data. We also notice that the coverage guarantee applies even when the calibration set has finite size \(n\), and we do not make any assumptions on what type of distribution it is (e.g. Gaussian), only that the distributions of calibration and test data are similar (exchangeable). For a more detailed introduction to conformal prediction including proofs and caveats, see Angelopoulos & Bates, 2021.3
Human-in-the-Loop Conformal Prediction
While the preceding introduction paints conformal prediction as a versatile tool (which it certainly is!), it comes with one major drawback. Having a set of likely outcomes is not the same as having a single outcome. Imagine heading out for lunch with several friends. If your group has suggested three different restaurants that everyone is happy with, you still don’t know where you’re having lunch that day! Making a decision requires cutting the list of possibilities down to a single selection and acting on it. Hence, we say that prediction sets are not inherently actionable.
Humans can serve as the final stepping stone, turning prediction sets into actionable decisions. At the start of this post we remarked on how humans express uncertainty. Thinking back to conformal prediction sets, we see that they mimic what humans do: larger sets signal greater uncertainty while providing alternative answers. This makes conformal prediction potentially a great fit for human-in-the-loop decision making systems. First, conformal prediction is used to generate prediction sets with a coverage guarantee. Then, a human makes the final decision informed by the model’s opinion. By working from an accurate short list of options, we may see improvement in the accuracy and speed of the human’s decisions. This type of human-AI team is promising for applications in healthcare where as a society we still want human doctors to make the final decision on diagnoses and treatments. Still, conformal sets could help doctors work faster and surface problems they may have missed on their own.
Another area of application is in banking where human underwriters make decisions on loan applications. For high-value loans, like mortgages, the risks of complete automation may be too high, but giving underwriters conformal prediction sets could again improve the decisions they make. Layer 6 models deployed at TD Bank have used conformal prediction in this way to help TD colleagues deliver better experiences to customers.
While we can imagine prediction sets assisting human decision makers, it is also possible they might hurt human performance from any number of unforeseen effects. Humans, after all, are much more complicated than machine learning models. Giving additional information through conformal sets may slow down decision making, as the person has more information to process. Sets could also be misused, or the coverage guarantee misinterpreted. As a final example, the model may simply be less accurate than the human on their own and mislead them.
Testing the usefulness of conformal prediction sets
Although hundreds of research works have been published in recent years on statistical analysis of conformal prediction, and on the design of score functions, \(s(x, y)\), to reduce conformal set sizes, no prior research has provided scientific evidence that humans actually benefit from the uncertainty quantification provided by conformal sets. Our work, published at ICML 2024, addresses this gap.4
We conducted a randomized controlled experiment with recruited participants to test the usefulness of conformal prediction sets along two axes – human accuracy and speed. As a control, one group of people were not given any help from a model, and as a baseline another group received prediction sets constructed by taking the top-\(k\) most likely model predictions – this method provides alternatives but does not quantify uncertainty since all sets are the same size. To control for the variable of coverage, the conformal sets were designed to have the same coverage rate as the top-\(k\) sets.
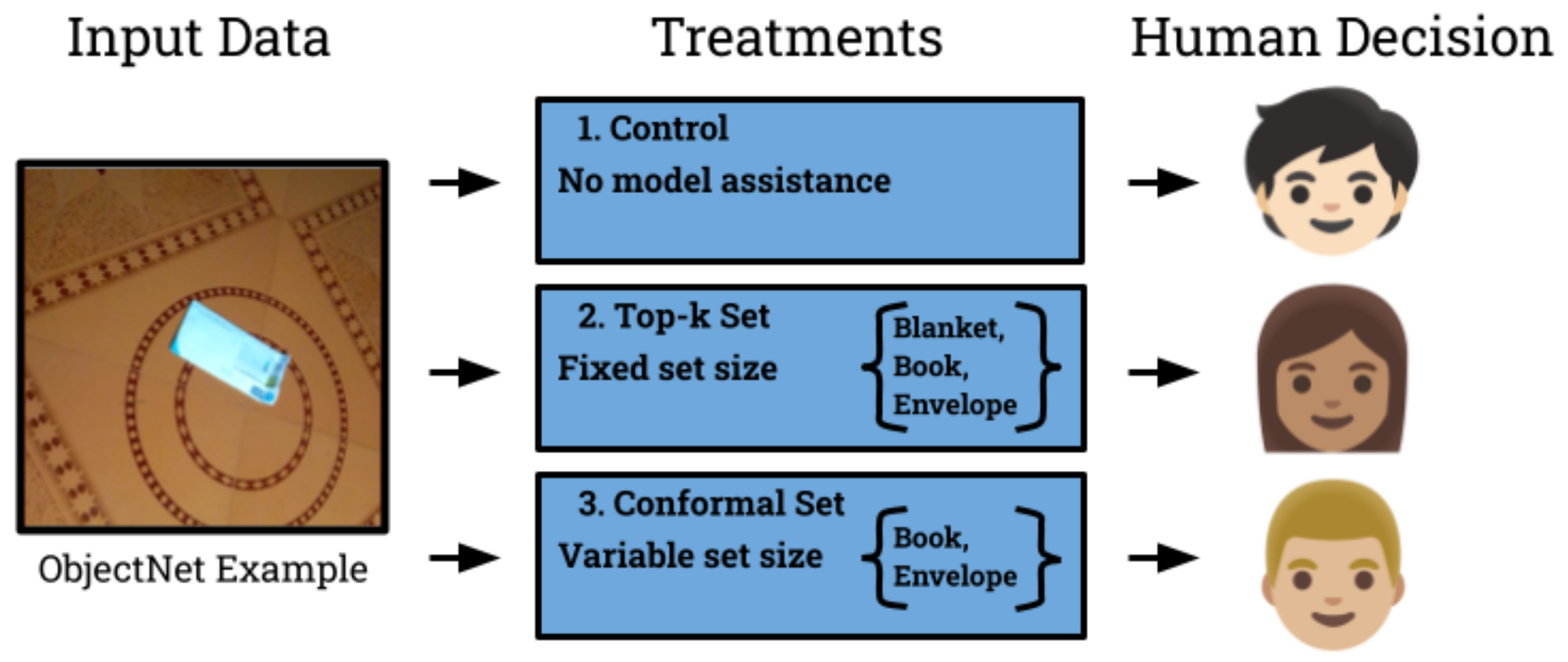
In total, we designed three distinct and challenging tasks that reflect real-world usecases of conformal prediction. Each was based on a common dataset from the machine learning literature for which pre-trained models were available.
- Image Classification is a task to identify the type of object in an image. Humans routinely identify objects from visual cues, such as traffic signs while driving. We used the ObjectNet dataset containing 20 different types of everyday items photographed from intentionally difficult viewpoints to represent this task.
- Sentiment Analysis aims to determine the emotion expressed in text. Humans constantly infer sentiments conveyed by others to understand context and communicate effectively. For this task we used GoEmotions, a dataset of English Reddit comments separated into 10 sentiment types.
- Named Entity Recognition tries to infer the meaning of proper nouns in text. When reading new content, humans often come across unfamiliar proper nouns and must infer their meaning from context. We constructed such a task using Few-NERD, a dataset of English sentences from Wikipedia, and used 20 classes of entities.
These three tasks provide three independent tests of the usefulness of conformal sets.
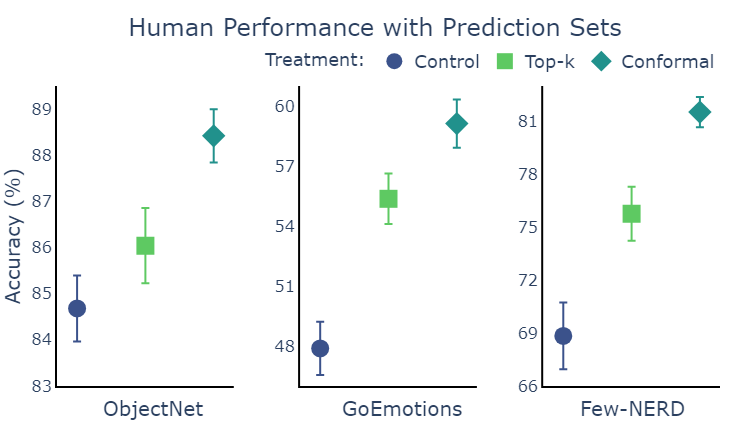
Conformal prediction sets improve human accuracy
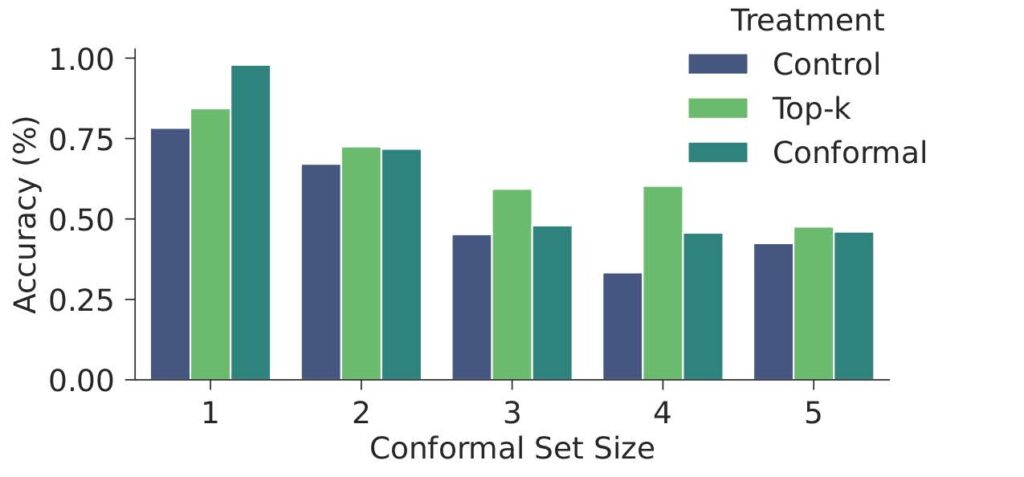
For each pair of task and treatment we recruited 50 unique people and measured their accuracy and speed in completing the task. Using hypothesis testing we can determine if there is a significant effect of the treatment on performance. Indeed, we found statistically significant evidence on all three tasks that conformal prediction sets led to increased accuracy compared to both the control, and to top-\(k\) sets. Because both types of prediction sets have the same coverage, there are only two differences between the methods to which we can ascribe the improvement: conformal sets quantify uncertainty, and are smaller on average.
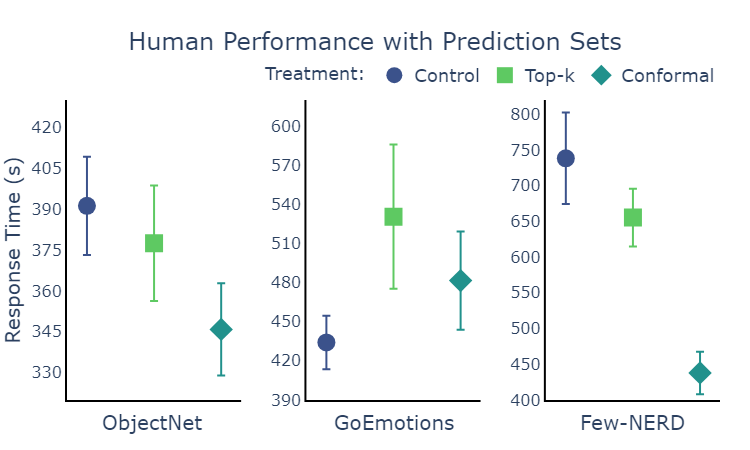
Unlike for accuracy, we found inconsistent results for speed. On one task the Control group was actually the fastest, but overall the results are consistent with the null hypothesis that there is no effect of the treatments on speed. The intuition that a shortlist of answers should speed up decisions clearly does not always hold. For instance, a shortlist may distract the user by giving them extra information to think through. However, we imagine that shortlists do become more useful as the overall number of classes to choose from increases.
Improving human-AI teams
Our experiments reveal several interesting interactions that inform how we design human-AI teams. For one thing, we would like to understand how humans interpret and make use of the uncertainty quantification provided by conformal sets. Since the control and top-\(k\) treatments do not distinguish examples by their difficulty, we can compare human accuracy across treatments conditional on conformal set size which acts as a proxy for the difficulty of each example. We observe that conformal sets improve human decision making most compared to other treatments when the model provides a singleton conformal set. Because conformal sets communicate uncertainty, humans learn to trust the model when it expresses certainty by giving a single option.
Ensembling effects
Above, we concluded that the combination of human and model (conformal treatment) outperforms humans alone (control) in terms of accuracy. Another relevant question is whether human-model teams outperform the model alone. Below we show this comparison in more detail using per-class accuracies for the image classification task. Notably, low model accuracy on a class (Bandage, Battery, Blanket, Bucket, Cellphone) tended to drag down the human-model team compared to humans alone. Poor model performance or biases against certain groups may not be completely overcome by humans. However, when the model outperformed the humans, the human-model team also tended to benefit, sometimes surpassing both individual partners (Backpack, Book, Bottle, Opener, Candle, Sandal). Hence there is a type of ensembling effect where one partner’s weaknesses can be corrected by the other.
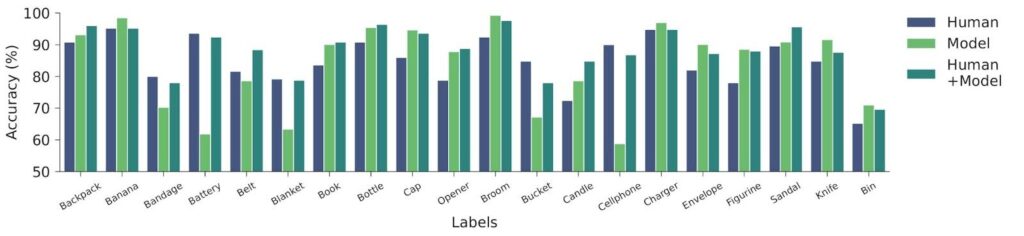
teams (the conformal treatment group).
Closing thoughts
Our ICML 2024 paper contains complete detail about these experiments along with additional insights. To wrap up, we showed that one of the most popular methods for uncertainty quantification in machine learning naturally fits with human-in-the-loop systems, and actually does improve decision making accuracy. Including a human into decision pipelines can mitigate some of the concerns around the trustworthiness of machine learning models. For example, more advanced machine learning methods are often less explainable, whereas humans could articulate their thought process even when aided by prediction sets. Neural networks are infamously susceptible to adversarial examples, which, by definition, do not fool humans, making a human-in-the-loop perhaps the most robust defense to adversarial attacks. Still, there are limitations to human-in-the-loop systems. On two out of three tasks, top-1 model accuracy was higher than what humans achieved (even with model assistance). We also found that when a model performs particularly poorly on groups within the data, prediction sets can drag down human performance on those groups. This could manifest as a transfer of biases from models to humans, and reinforces that the fairness of models still needs to be considered even with a human-in-the-loop.
Read about our research on the fairness of conformal prediction here
References
- Vovk, V., Gammerman, A., and Shafer, G. Algorithmic Learning in a Random World. Springer, 2005. ↩︎
- Guo, C., Pleiss, G., Sun, Y., and Weinberger, K. Q. On calibration of modern neural networks. ICML 2017. ↩︎
- Angelopoulos, A. N. and Bates, S. A gentle introduction to conformal prediction and distribution-free uncertainty quantification. arXiv:2107.07511, 2021. ↩︎
- Cresswell, J. C., Sui, Y., Kumar, B., and Vouitsis, N. Conformal Prediction Sets Improve Human Decision Making. ICML 2024. ↩︎



