In this blog, we dive into some puzzling observations in few-shot learning: despite having access to less information, the simple scheme of pre-training and fine-tuning has been shown to support better adaptation performance compared to more sophisticated meta-learning algorithms. We hypothesize the reason for these observations, and propose a solution which unlocks the full potential of meta-learning on few-shot learning problems.
Background & Introduction
Few-shot Learning
If you know how to drive a car on the highway, you can probably jump in a golf cart on grass, or a dune buggy on sand and very quickly feel comfortable behind the wheel. Although each of these vehicles will have different handling, acceleration, and traction, you can easily adapt the inputs you would use driving a car to manage these new scenarios with only a few seconds of test driving. This is an example of few-shot learning, where an intelligent agent is required to learn and adapt to a new challenge in a fast, efficient, and flexible manner. Humans can inherently leverage their general knowledge and past experience to handle new situations on a daily basis, and hence few-shot learning is regarded as one of the milestones in the pursuit of artificial general intelligence.
In machine learning, few-shot learning requires a model to learn to perform a previously unseen task based on only a few examples. This contrasts with the typical machine learning pipeline where a model is trained on a single dataset for a single task; any other task requires a completely separate model. For solving general few-shot learning problems, two of the most popular research directions that have been explored are meta-learning, and pre-training and fine-tuning.
Meta-learning
Meta-learning represents a strong class of approaches for solving few-shot learning tasks. Specifically, meta-learning explores the possibility of enabling the model to learn-to-learn. In meta-learning, individual tasks serve a similar role as individual data points in conventional machine learning. Under the meta-learning setup, two sets of tasks are prepared: meta-training tasks to train the model, and meta-testing tasks to evaluate the model. The overall goal of meta-learning is to train and update a model throughout its learning procedures on the meta-training tasks such that the optimised model can quickly adapt to new unseen tasks, as evaluated by its performance on the meta-testing tasks.
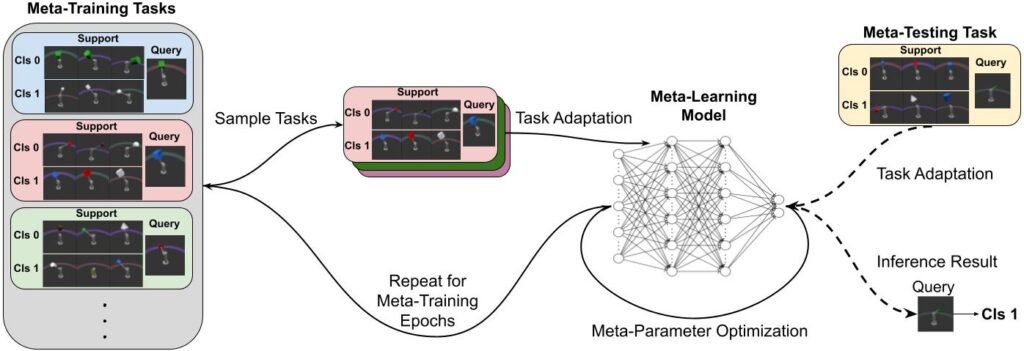
Specifically, consider a parameterized machine learning model \(f(\phi, \theta)\), with \(\phi\) being the collection of meta-parameters shared across different tasks, and ɵ being the task-specific parameters to be adapted on each individual task. The general meta-training process optimizes the model’s meta-parameters \(\phi\) over the meta-training tasks, on a two-level optimization scheme. Specifically, on each meta-training task, the model performs adaptation on the task-specific \(\theta\), resulting in a task-level loss. Then, a global-level loss is computed aggregating all the task-level losses within the meta-training set. The parameters \(\phi\) are updated to optimize this global loss. After the meta-training stage, we fix \(\phi\) to the optimized value, and adapt the model to each meta-testing task by tuning \(\theta\) on a small portion of the task’s datapoints, which are called the few-shot examples.
Meta-learning has been one of the main forces for solving few-shot learning problems. In one of the most popular meta-learning approaches, Model-Agnostic Meta-Learning, \(\phi\) is the collection of initialization values for all the parameters in the model, while \(\theta\) represents the set of finalized values of these model parameters after being optimized on a given task.
Pre-training and Fine-tuning
Pre-training and fine-tuning is a general scheme used for model adaptation under various scenarios. For few-shot learning in particular, it has been adapted by splitting the training data to use a portion for meta-learning (i.e. the meta-training set). Specifically, in the pre-training stage (equivalent to the meta-training stage for meta-learning), all the data points from different meta-training tasks are aggregated into a large dataset, ignoring the labels and task identities for different tasks.
Like for meta-learning, the parameterized model \(f(\phi, \theta)\), has model parameters partitioned into two sets: the general-purpose parameters \(\phi\), and the task-specific parameters \(\theta\). For the pre-training stage, no distinction is made between different tasks (i.e. the meta-training tasks). The set of parameters \(\phi\) is trained and optimized on the entire aggregated dataset using a single loss function (e.g. a self-supervised loss). The main difference between this pre-training stage and meta-training is that \(\phi\) is directly updated in a single supervised/unsupervised step, instead of the two-level optimization meta-training uses. In the fine-tuning stage, the task-specific parameters \(\theta\) are fine-tuned to adapt to testing tasks (i.e. the meta-testing tasks).
The conventional choices of \(\phi\) and \(\theta\) in the pre-training and fine-tuning scheme are often different from meta-learning. For example, in classification tasks \(\phi\) is often the collection of parameters of an encoder that maps the inputs to a general-purpose embedding space, while \(\theta\) is the collection of parameters in an adaptation layer that maps the embedding space to the outputs.
Less Information is Better?
The Curious Case of Degraded Performance from Meta-learning
As elaborated above, pre-training and fine-tuning is a much simpler scheme compared to meta-learning, largely because it neglects two crucial sources of information: identities of different meta-training tasks; and labels within meta-training tasks. Regardless, multiple recent research studies suggest that the much simpler pre-training and fine-tuning approach sometimes achieves even better results than more complex meta-learning algorithms. This finding is unexpected, and perhaps even puzzling, as it implies that information about training tasks and their labels may be irrelevant to achieving high few-shot learning performance.
Gap in State-of-art Few-shot Learning Benchmarks
We hypothesize that this observation can be attributed to the lack of task diversity in many popular few-shot learning benchmarks. For instance, in canonical few-shot learning datasets such as Omniglot, miniImageNet, and CIFAR-FS, the distinct tasks differ solely in that their targets belong to distinct, non-overlapping sets of object classes. In essence, these few-shot learning tasks all share the same nature: main object classification. Hence, there is one degenerate strategy for solving all these tasks simultaneously without the need for individually identifying each task or relying on meta-training labels: compare the main object in the query image to the main objects in the few-shot support images, and assign the class label based on similarity to support images. This strategy can be easily achieved through pre-training with contrastive learning using common image augmentations like rotation and cropping which preserve the semantics of the main object, while discarding other factors such as orientation and background. Given the shared nature of tasks on these specific benchmarks, it is not surprising that a single pre-trained encoder can perform competitively against meta-learning methods.
To rigorously challenge a model’s adaptation ability achieved by either meta-learning or pre-training and fine-tuning, we advocate for the establishment of few-shot learning benchmarks that include tasks with fundamentally distinctive natures. Specifically, we consider tasks beyond main object classification, such as identifying object orientation, background color, ambient lighting, or attributes of secondary objects in the image. At the same time, models should be agnostic to the nature of the evaluation tasks. Such setups can reveal the model’s true capacity to learn strictly from the few-shot samples, with task identification expected to be an essential component.
DRESS: Disentangled Representation-based
Self-Supervised Meta-Learning for Diverse Tasks
We introduce DRESS, our task-agnostic Disentangled REpresentation-based Self-Supervised meta-learning approach. DRESS leverages disentangled latent representations of input images to construct self-supervised few-shot learning tasks that power the meta-training process. Within disentangled representations, different dimensions depict distinct aspects of the input data. Using these representations, the sets of self-supervised tasks we can construct are naturally diversified, requiring distinct decision rules to solve. When using these tasks for meta-training, the model can digest each factor of variation within the data, and therefore learns to adapt to unseen few-shot tasks regardless of their contexts, natures, and meanings.
Furthermore, we also propose a class-partition based metric for quantifying the task diversity directly on the input spaces. Through our exploration, we advocate for a re-examination of proper setups for task adaptation studies, and aim to reignite interest in the potential of meta-learning for solving few-shot learning tasks via disentangled representations.
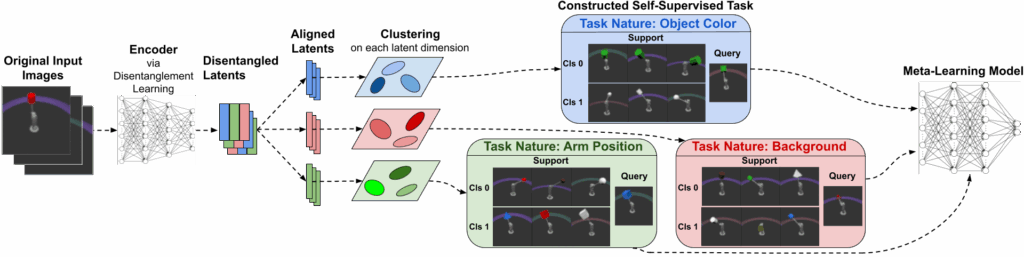
We introduce our proposed approach, DRESS, stage-by-stage as follows.
Encoding Disentangled Representations
First, all images available for meta-training are collected, and used to train a general purpose encoder with the objective of producing disentangled representations. We then use the trained encoder to encode the images to obtain their disentangled latent representations.
Aligning Latent Dimensions
After collecting the disentangled representations for all the training images, we align the latent dimensions of representations across images, corresponding to the semantic meaning of each latent dimension. After alignment, a given dimension in the latent space conveys the same semantic information across all images (e.g., main object color, background color, lighting color).
Clustering Along Disentangled Latent Dimensions
We perform clustering on each dimension over the latent values. Since dimensions are disentangled and aligned, clustering each latent dimension produces a distinct partition of the entire set of inputs that corresponds to one specific semantic property.
Forming Diverse Self-Supervised Tasks
Finally, we construct self-supervised learning tasks using cluster identities as the pseudo-class labels. We create a large number of few-shot classification tasks under each disentangled latent dimension by first sampling a subset of cluster identities as classes, and then sampling a subset of images under each class as the few-shot support samples and query samples.
Task Diversity based on Class Partitions
We advocate for a task diversity metric that is not tied to any specific embedding space, but is instead linked to the original input space and is based on the task’s class partitions.
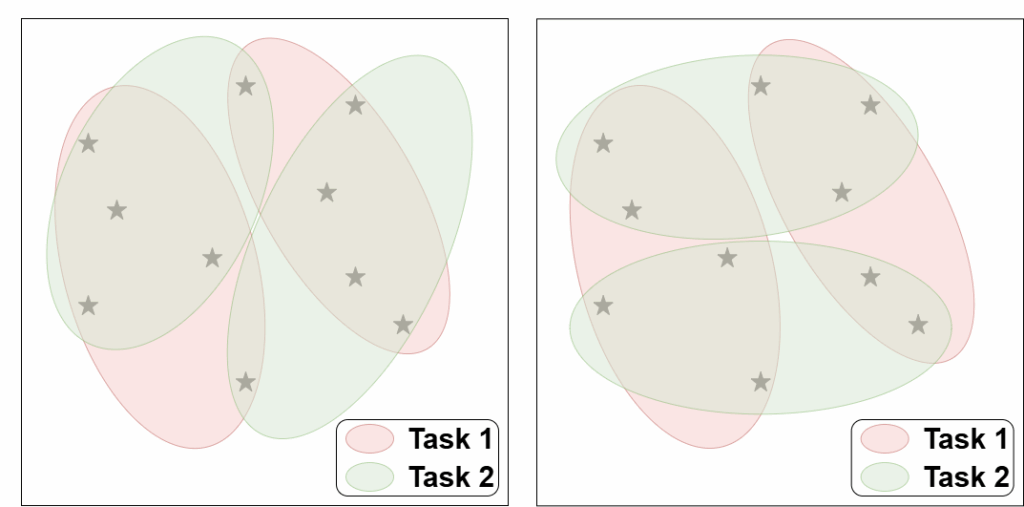
Consider two classification tasks defined on the same inputs. Each task partitions the dataset based on class identities. Our task diversity metric is computed using these class-based partitions. First, we match subsets between class partitions of the two tasks to maximize the pairwise overlaps, which can be achieved using methods such as bipartite matching. For each matched pair of subsets, we then compute the intersection-over-union (IoU) ratio. Finally, we calculate the average IoU value across all subset pairs across the two partitions. A low average IoU indicates that the two class-based partitions differ significantly, suggesting that the two tasks are relatively diverse tasks. We note that during the step of relabeling the classes, the semantic information of the class concepts in each task is lost. Therefore, the proposed metric only quantifies task diversity from the function mapping perspective. Nonetheless, learning to jointly solve tasks that are diversified in their function mappings (as measured by our metric) has been shown to promote the development of better adaptation capacity.
Effective Few-Shot Learning on Diverse Tasks
We consider datasets with a large number of independent factors of variations, including well-curated synthetic datasets and a realistic complex dataset, as follows:
- Well-Curated Datasets
- SmallNORB: Images with a single gray-scale color channel, capturing objects under 5 generic categories at different camera angles and lighting conditions.
- Shapes3D: Images capturing objects of different shapes, colors, scales, and orientations, with surroundings composed by changing floor and wall colors.
- Causal3D: Images capturing objects at different positions (measured by positional coordinates), under changing floor and spotlight colors.
- MPI3D: Images capturing a robot arm grabbing an object. The robot arm has two degrees of freedom for movement, while the object varies in shape, size, and color. The camera height and background also change independently.
- Realistic Complex Datasets
- CelebA: A collection of celebrity face photos with annotations for many types of facial features.
- LFWA: Labelled faces in the wild with attributes dataset, including faces of public figures captured under non-controlled settings, with binary facial attributes extracted from a vision model to serve as the facial recognition benchmark.
Across these datasets, we adapt DRESS to two different encoder architectures based on VAEs and diffusion to demonstrate DRESS’s flexibility in obtaining disentangled representations.
Task Adaptation Performance
On well-curated datasets, DRESS consistently achieves the best few-shot adaptation performance among unsupervised methods, with an exception on the Shapes3D dataset. Pre-training and fine-tuning is not on par with meta-learning approaches when benchmarked on more challenging and diverse tasks, which is in line with our intuition that its performance should suffer since it ignores highly relevant information on task identities and labels. As DRESS uses disentangled representation learning to construct diversified pre-training tasks, it obtains superior results across these datasets and task setups which have similarly diverse objectives.
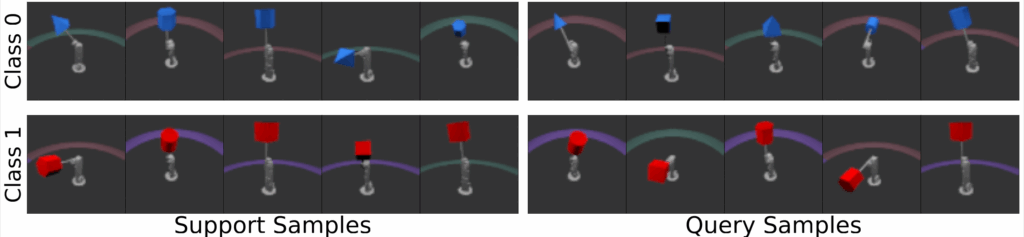
We provide visualizations of tasks constructed by DRESS here.
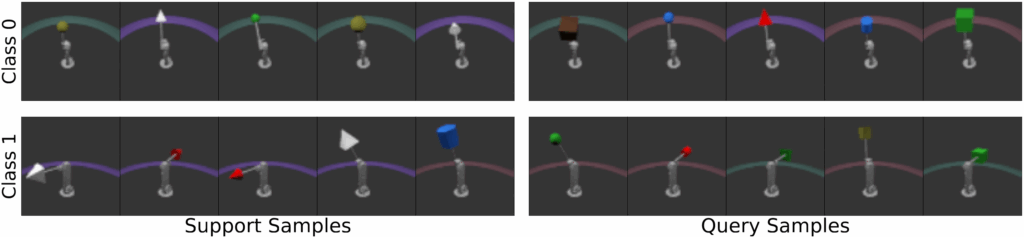
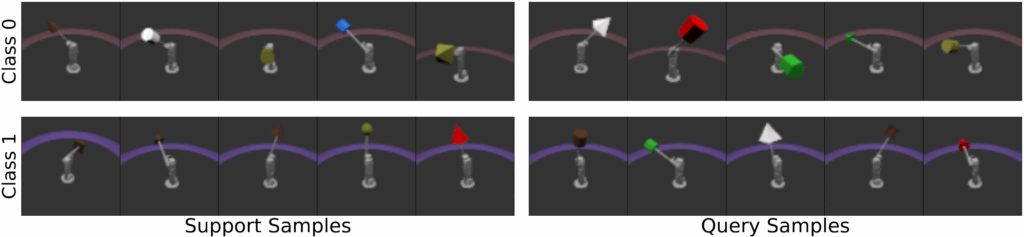
Meanwhile, on the real-world dataset CelebA, DRESS outperforms all unsupervised/self-supervised methods on most experiment setups, excelling at capturing secondary features (i.e. hair features) beyond primary facial attributes. To test the model’s cross-domain adaptation ability, we adapt each model to few-shot learning tasks created from the LFWA dataset. Under this setting, DRESS also excels across unsupervised/self-supervised baselines, illustrating the robustness of the learned features supported by DRESS.
Further Explorations
Through our exploration in this project, we have noticed that disentangled representation learning still has room for improvement, especially for complex images, in areas including: modeling fine details within images, filtering out irrelevant background noise from identified factors of variations, latent quantization, faithful reconstruction, hyper-parameter tuning, and so on. The quality of such disentangled representations directly affects the meta-learning performance from DRESS.
On the other hand, we emphasize that DRESS is not restricted to image data, but has the potential to be adapted to other data modalities, for example on natural language (with potential disentangled factors of variations such as semantics, sentiments, or tense), tabular data (if table columns can be further grouped or divided as independent varying factors), and audio (e.g. content, timbre, rhythm, temporal dynamics, or background noise). Essentially, DRESS supports maximal extraction of information and pattern from unlabelled data for supporting fast adaptation within a foundational model.



